Congruent Triangles Coloring Activity Dinosaur Answer Key

Have you ever picked up two items and found they fit together just right, almost as if they were made for each other? Maybe two pieces of a puzzle, or perhaps two slices of bread from the same loaf? Well, that feeling of things fitting perfectly, of being the same in every way, is actually a pretty good way to think about what "congruent" means in the world of shapes. It’s a simple idea, yet it’s a big part of how we understand shapes and their relationships. This idea, so it's almost, helps us see how different parts of a picture or a design can be exact copies of each other, even if they're turned around or flipped over.

When we talk about shapes being "congruent," we are really just saying they are identical. They have the same exact shape and the same exact size, too. Think about it like this: if you could pick one shape up and put it right on top of another, and they lined up perfectly, then you'd have congruent shapes. This concept is super important in geometry, which is, you know, the study of shapes and space. It helps us figure out if things are truly equal, not just similar, and that can be pretty useful for all sorts of things, as a matter of fact.

Now, imagine taking this idea of perfectly matching shapes and turning it into something fun and engaging, like a coloring activity. Picture a sheet filled with shapes, some of which are exact duplicates of others, just waiting for you to find them. And what if those shapes were part of a bigger picture, maybe even a dinosaur? This kind of activity, which might be, helps people, especially younger learners, really get a handle on what congruence means by seeing it firsthand and getting to interact with it. It’s a hands-on way to explore geometry, and it comes with a helpful answer key, too, just so you can check your work.

What Does "Congruent" Really Mean?
How Do Shapes Become Congruent?
Why Are Congruent Triangles So Important?
Putting It All Together with Your Coloring Activity
- Checking Your Work with the Dinosaur Answer Key
What Kinds of Things Can Be Congruent?
Is This Triangle Activity Right for You?
Getting Started with Your PDF Resource
- Tips for Using Your Answer Key
Making Learning Fun with Congruent Shapes

What Does "Congruent" Really Mean?

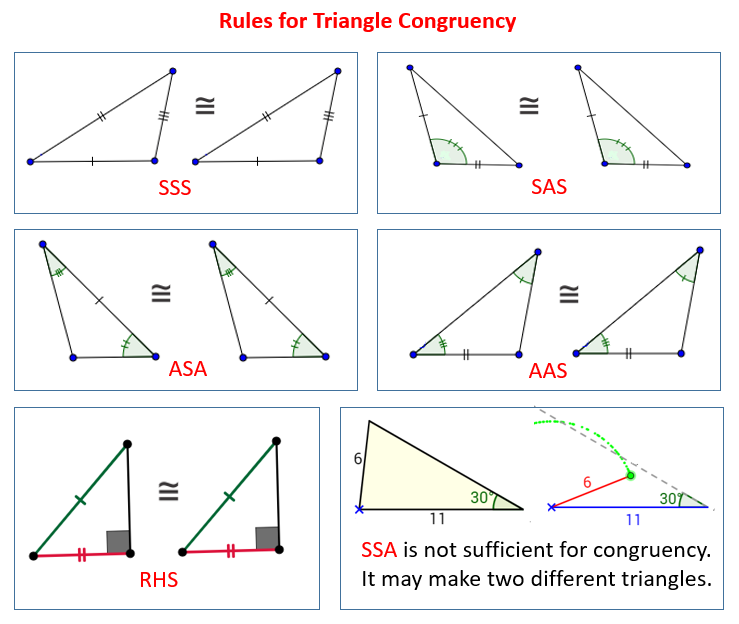
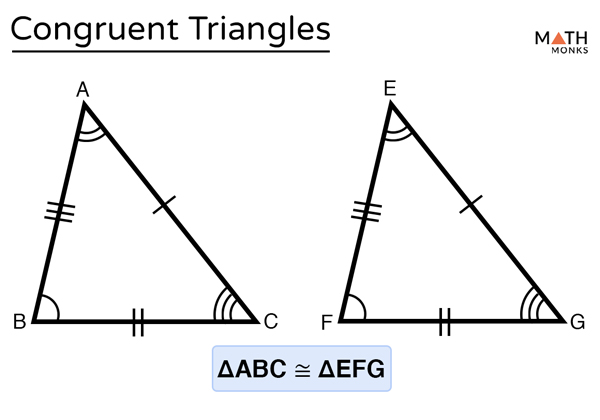
The word "congruent" itself has a pretty straightforward meaning, when you get right down to it. It simply means that things are the same. In geometry, specifically, it means that two figures or objects share the exact same shape and the exact same size. Imagine, for instance, two identical cookies from the same batch. If you put one on top of the other, they would line up perfectly, wouldn't they? That's what we mean by congruent. They are, in a way, superposable, which is a fancy way of saying they can be placed exactly over each other and match up everywhere. This idea applies to all sorts of geometric figures, from simple lines to complex shapes, and it's, you know, a basic building block for understanding more advanced concepts.

My text tells us that "congruent means identical in shape and size." It also says that if you "place one slice of bread over the other, you will find that both the slices are of equal shape." This is a really good everyday example of congruence. They are not just similar, they are exactly the same. So, when you see a shape and then another one that looks just like it, and you can tell that if you picked one up, it would fit right on top of the other, then you are looking at congruent figures. It’s a pretty simple concept, honestly, but very powerful for describing how shapes relate to each other. You could say, too it's almost, that they are perfect twins.

The concept extends beyond just looking alike. It's about a precise match. If you have two triangles, for example, and they are congruent, it means that every side of one triangle has a matching side of the same length on the other triangle. And, of course, every angle in one triangle would have a matching angle of the same measure in the other. They are, essentially, perfect copies of each other. This is, you know, a pretty important distinction, because shapes can look similar without being truly congruent. This is why, in some respects, the definition is quite strict.

How Do Shapes Become Congruent?

Shapes don't really "become" congruent in the sense of changing their nature; rather, we recognize them as congruent even if they've been moved around. My text mentions that "when one shape can become another using turns, flips and/or slides, then the shapes are congruent." These actions—turns, flips, and slides—are called transformations in geometry. They are movements that don't change the size or shape of the figure itself. So, if you take a triangle and simply slide it across a page, it's still the same triangle, just in a different spot. It's still congruent to its original position, obviously.

Think about a turn, or a rotation. If you spin a triangle around a point, it's still the same triangle, isn't it? It hasn't grown bigger or shrunk smaller. It hasn't changed its angles or side lengths. It's just facing a different direction. This is, you know, a classic example of how congruence holds true even after a shape has been rotated. The shape still, basically, holds its original form and size, no matter how much you spin it around. This means that if you have two triangles that are congruent, one might be a turned version of the other, and they are still a perfect match.

A flip, or a reflection, is another way shapes can be moved without losing their congruence. Imagine looking at yourself in a mirror. Your reflection is a mirror image of you, right? It's the same size, the same shape, just reversed. In geometry, a flip means creating a mirror image of a shape. If you flip a triangle over a line, the new triangle is still congruent to the original one. It's just, you know, facing the opposite way, but its dimensions haven't changed at all. This is, frankly, a pretty neat trick that shapes can do while staying identical.

Finally, a slide, also known as a translation, is perhaps the simplest transformation. It's just moving a shape from one place to another without turning it or flipping it. If you pick up a piece of paper and just move it across your desk, it's still the same piece of paper. It hasn't changed its size or shape. It's still congruent to where it was before. These transformations are, in fact, how we often see congruent shapes in the real world: they might be in different spots or orientations, but they are still exact duplicates of each other. This is, you know, pretty much the core idea behind how we identify matching shapes in activities like the coloring one.

Why Are Congruent Triangles So Important?

Triangles are, in a way, the superheroes of geometry. They are the simplest shapes that can be rigid, meaning they hold their form. Think about how bridges and buildings often use triangular structures; it's because triangles are incredibly stable. When we talk about congruent triangles, we are talking about two triangles that are exact duplicates of each other, right down to every side and every angle. This is, arguably, one of the most fundamental concepts in geometry because if you can prove two triangles are congruent, you automatically know a whole lot about their corresponding parts without even measuring them all. This saves a lot of time and effort, as a matter of fact.

The importance of congruent triangles extends into many areas, from architecture to engineering and even art. If you're building something where precision matters, knowing that two parts are congruent means they will fit together perfectly, just like you'd want them to. For learning, especially with something like a coloring activity, focusing on triangles helps simplify the concept of congruence. Triangles are, you know, basic enough that they are easy to work with, but complex enough to show off all the rules of congruence. This makes them a really good starting point for young learners.

For instance, in the context of a coloring activity, you might be given a set of triangles and asked to find all the ones that are congruent to a particular example. Because triangles are so well-defined by their sides and angles, it becomes a clear task to spot the matching ones, even if they've been turned or flipped. This kind of visual search and matching, which is, you know, pretty much what a coloring activity involves, helps solidify the abstract idea of congruence in a very concrete way. It's a very practical application of the concept, honestly.

Putting It All Together with Your Coloring Activity

So, how does all this talk about congruence connect with a fun coloring activity? Well, imagine a page full of different shapes, and among them are several triangles that are exactly the same, even if some are upside down or facing another way. The goal of a congruent triangles coloring activity is usually to identify these matching pairs or groups of triangles. You might be asked to color all the congruent triangles the same color, or perhaps to find all the triangles congruent to a specific "target" triangle. This kind of hands-on work, you know, really helps to make the concept stick. It’s a very visual way to learn, and that can be pretty helpful for many people.

The "coloring" part of the activity isn't just for fun; it serves a real purpose. By actively coloring shapes, you are engaging with the material in a different way than just looking at it or writing about it. It forces you to really observe the shapes, compare their sizes and forms, and make decisions about which ones are truly identical. This kind of active learning, which is, you know, quite effective, helps to build a stronger mental picture of what congruence looks like. Plus, it's a bit more enjoyable than just, say, filling out a worksheet, isn't it? It can be, you know, quite a relaxing way to learn.

The dinosaur theme adds another layer of engagement, too. For many, dinosaurs are, you know, pretty fascinating creatures, and incorporating them into an activity can make learning feel less like a chore and more like an adventure. Maybe the congruent triangles form parts of a dinosaur's scales, or its teeth, or its footprints. This creative context makes the learning experience more memorable and enjoyable, especially for younger students. It's a way to, basically, make the abstract idea of geometry feel more tangible and exciting. You might even say it's, in a way, a bit of a prehistoric geometry lesson.

Checking Your Work with the Dinosaur Answer Key

Any good learning activity, especially one involving identification, comes with a way to check your answers. That's where the "dinosaur answer key" comes in. After you've spent time carefully looking at the triangles and coloring the ones you believe are congruent, you can then refer to the answer key to see how well you did. This self-correction step is, you know, pretty important for learning. It allows you to immediately see if your understanding of congruence is accurate and to correct any mistakes right away. It's, in short, a valuable tool for feedback.

The answer key for a congruent triangles coloring activity, especially one with a dinosaur theme, will typically show the correctly colored triangles or highlight the congruent pairs. This way, you can compare your colored sheet with the answer key and identify any discrepancies. If you missed a congruent triangle or incorrectly colored one that wasn't congruent, you can then go back and figure out why. This process of reviewing your work and understanding where you went wrong is, you know, quite a powerful way to learn and reinforce the concept. It's like having a little helper right there with you, basically, guiding your learning.

Having an answer key means you don't have to wait for someone else to tell you if you're right or wrong. You can take charge of your own learning, which is, you know, pretty empowering. It helps build confidence as you see your understanding grow. And for an activity that's, like, visually driven, an answer key that shows the correct coloring or matching is really, really helpful. It gives you a clear visual guide, which can be, you know, pretty much what you need to confirm your understanding of the congruent triangles. It's a very direct way to get feedback, too.

What Kinds of Things Can Be Congruent?

The idea of congruence isn't just for triangles or the dinosaur coloring activity. My text points out that "congruence can be applied to line segments, angles, and figures." This means that the concept of being "identical in shape and size" extends to the most basic elements of geometry. For example, two line segments are congruent if they have the exact same length. It doesn't matter if one is horizontal and the other is vertical; if their lengths are equal, they are congruent. This is, you know, pretty straightforward, honestly.

Similarly, angles can be congruent. If you have two angles, and they both measure, say, 45 degrees, then they are congruent. Their orientation or where they are placed on a page doesn't change their congruence. It's all about their measure, or how wide they open up. This applies to all sorts of angles, whether they are acute, obtuse, or right angles. As a matter of fact, knowing that angles are congruent is a huge part of proving that larger shapes, like triangles, are also congruent. It's, you know, a very basic building block.

And, of course, "figures" in general can be congruent. This includes everything from simple squares and circles to more complex polygons and even three-dimensional objects. If you have two squares, and they both have sides of the exact same length, then they are congruent. If you have two circles with the exact same radius, they are congruent. The principle is the same: if you can place one figure precisely over the other and they match up perfectly, then they are congruent. It's, you know, a very broad idea that covers a lot of ground in geometry.

The beauty of this concept is that it gives us a precise way to compare geometric objects. Instead of just saying "they look alike," we can say "they are congruent," which means they are, in fact, identical in every measurable way. This precision is, you know, pretty important in many fields, and it's a core idea that the congruent triangles coloring activity helps to teach. It's about recognizing that exact match, whether it's for a line, an angle, or a whole shape. This is, basically, what makes geometry so logical and predictable.

Is This Triangle Activity Right for You?

Thinking about whether a "congruent triangles coloring activity dinosaur answer key pdf" is a good fit for your needs really depends on what you're hoping to achieve. If you're looking for a fun, hands-on way to introduce or reinforce the concept of congruence, especially for younger learners or those who benefit from visual aids, then, you know, this kind of activity is probably a really good choice. It takes an abstract mathematical idea and makes it tangible and engaging, which can be, honestly, pretty helpful for many students. It’s a very direct way to interact with the concept.

For educators, this kind of activity can be a great addition to a geometry lesson. It provides a break from traditional worksheets and offers a creative outlet while still teaching a core concept. It can be used for individual practice, as a group activity, or even as a quiet assessment. The fact that it comes as a PDF also means it's easily accessible and printable, which is, you know, pretty convenient for classroom use or for learning at home. It allows for, basically, a lot of flexibility in how it's used.

For parents looking for supplemental educational materials, this type of activity offers a way to support their child's learning outside of school. It's something you can do together, which can be, you know, pretty rewarding. The coloring aspect makes it less intimidating than a typical math problem, and the dinosaur theme adds an element of fun that can keep kids interested. It’s a very low-pressure way to explore geometry, and that can make a big difference for how a child feels about math. You might find, as a matter of fact, that it sparks a new interest.

Ultimately, if your goal is to make learning about shapes and their properties more enjoyable and accessible, then an activity like this is, you know, pretty much what you're looking for. It combines visual learning, active engagement, and a clear way to check understanding, all wrapped up in a theme that many find exciting. It's a way to learn without it feeling like work, which is, in a way, the best kind of learning there is. You could say, too it's almost, a perfect blend of education and entertainment.

Getting Started with Your PDF Resource

One of the great things about resources like the "congruent triangles coloring activity dinosaur answer key pdf" is how easy they are to use. Since it's a PDF, you can typically download it instantly after getting it. This means you don't have to wait for anything to be shipped, and you can get started almost right away. All you usually need is a computer or tablet and a printer, if you want a physical copy. This accessibility is, you know, pretty convenient, especially when you're ready to learn right now. It's a very direct way to access materials, honestly.

Once you have the PDF file, you can open it with any standard PDF reader. From there, you have the option to print out as many copies as you need. This is particularly useful for teachers who might want to print a copy for each student in their class, or for parents who want to print multiple copies for siblings or for repeated practice. The digital format gives you a lot of flexibility, which is, you know, pretty much what you want in a learning tool. You can, for example, save it and use it again later, too.

Before you start the coloring activity itself, it's a good idea to, basically, take a moment to look over the instructions. Make sure you understand what you're supposed to do: are you coloring all congruent triangles the same color? Are you identifying pairs? Knowing the goal clearly from the start will help you get the most out of the activity. It's a pretty simple step, honestly, but it can make a big difference in how well the activity goes. You want to be, you know, pretty clear on the task at hand.

Tips for Using Your Answer Key

The answer key is a really valuable part of this congruent triangles coloring activity, and using it well can boost your learning. First, it's usually best to try to complete the coloring activity on your own before looking at the answer key. This gives you a chance to really think through the problems and apply your understanding of congruence. It's like, you know, trying to solve a puzzle before looking at the picture on the box. The effort you put in beforehand makes the learning from the answer key much more meaningful. It’s, in a way, about building your own understanding first.

When you do use the answer key, don't just glance at it and move on. Take your time to compare your work with the correct answers. If there's a difference, try to figure out why. Did you miss a triangle? Did you misidentify one? Understanding your mistakes is, you know, a pretty important part of learning. It helps you see where your mental model of congruence might need a little adjustment. This reflective process is, basically, where the real learning happens. You might find, as a matter of fact, that a small adjustment makes a big difference.

Another good tip is to use the answer key as a learning tool, not just a grading tool. If you're struggling with a particular type of congruent triangle, use the answer key to see the correct identification and then try to understand the characteristics that make it congruent. This can help you recognize similar shapes more easily in the future. It's, you know, pretty much like having a personal tutor showing you the right way. This kind of focused review, you know, can really help solidify your grasp of congruent shapes. It's a very practical approach, too